Zipf’s law, and the family of associated power laws, which govern the frequency distribution of words in natural language, and many other things, are well known in the information sciences as the foundations of bibliometrics.
An intriguing new study by a group of physicists from Oxford, Paris, and Portsmouth, reported in a paper in the physics arXiv, Statistical Patterns in the Equations of Physics and the Emergence of a Meta-Law of Nature, examines the application of Zipf’s law to the symbols used in the equations of mathematical physics, treating each symbol and mathematical operator in the equations as a word and ranking their frequency. Three sets of equations were analysed: one derived from The Feynman Lectures on Physics, one derived from Wikipedia’s List of scientific equations named after people, and one derived from the Encyclopaedia Inflationaris review of inflationary cosmology. In each case, a Zipfian distribution, as shown below, was found, as it was in smaller subsets of equations relating to particular physics issues.
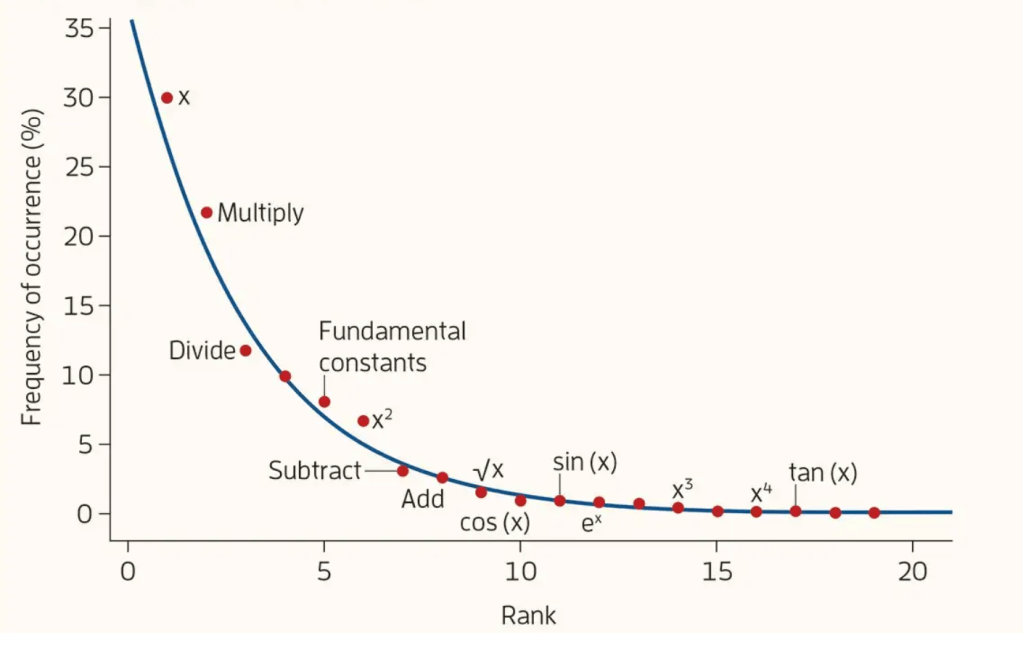
At first sight, this might not seem surprising. Mathematical notations are derived by humans for the communication of mathematical ideas; with the exception of some of the oldest notations, we know when, and by whom, they were devised and first used. We might perhaps expect that they would follow the same patterns as the words used for communication of non-mathematical concepts.
However, there may be more to it than this. The study is not of mathematical notations and communication generally, but of the set of mathematical notations used to capture the essence of the world, through the equations of physics. Following remarks in the original paper, a commentary article in New Scientist puts forward contrasting two viewpoints. Perhaps this pattern is saying something about how reality actually works, the overarching pattern that the equations follow also containing information about the nature of reality; a new meta-law of physics. Or perhaps these results could simply be a statistical by-product of physicists aiming to express their mathematical ideas succinctly, as with any other language.
I tend to favour the latter explanation, having tentatively suggested in a previous post that mathematical innovation is the result of the discovery of entities and relations in a Popperian World Three of human-created mathematical knowledge. It seems reasonable that such discoveries and innovations would be expressed in a language having a similar structure to other human languages. But this leaves unanswered Eugene Wigner’s complaint about the unreasonable effectiveness of mathematics in explaining the physical world. Does this newly discovered Zipfian structure of the mathematical basis of physics contribute to answering Wigner? An intriguing prospect indeed.
References
Andrei Constantin, Deaglan Bartlett, Harry Desmond, and Pedro G. Ferreira. Statistical Patterns in the Equations of Physics and the Emergence of a Meta-Law of Nature. physics>arXiv:2408.11065, 12 August 2024
Alex Wilkins. The laws of physics appear to follow a mysterious mathematical pattern. New Scientist, 21 October 2024.
